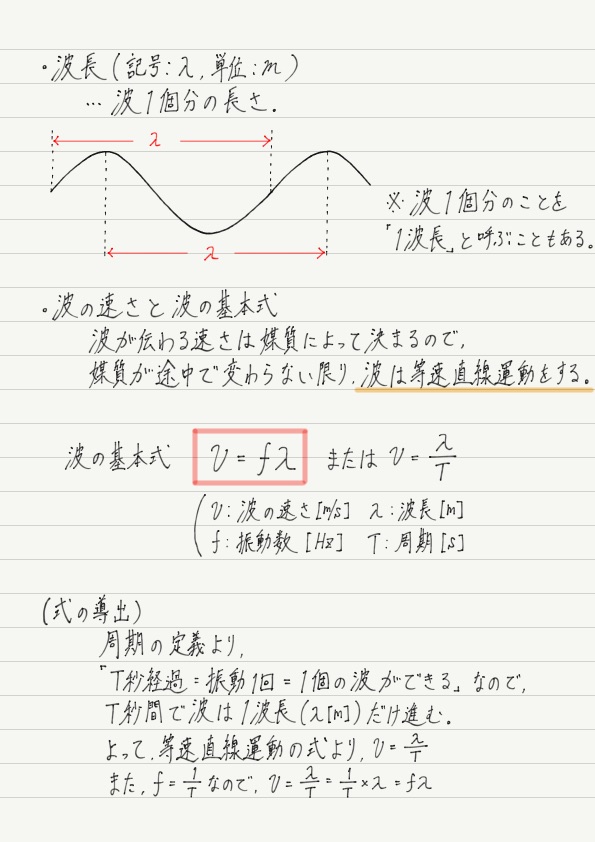
① 「波は、進む」 ということ。 当たり前なのだけど、水面に小石を落とせば、波周囲へだんだん広がっていく=波は進んでいます。つまり、波はボールを投げるのと全く同じように、 1回振動した後の状態を図3に示す.ここで,波長 m,振動数 Hzとする.波源が1回振動すると,波は1波長分,すなわち m進む.1秒間に振動する回数は 回であるので(振動数=1波の速さの求め方ってこの公式を使いますよね?? この2つのどちらかを使えばいいのですか? それとも問題によって使い分けをしないといけないのですか?? 物理が本当に分からなくて💦教えて頂
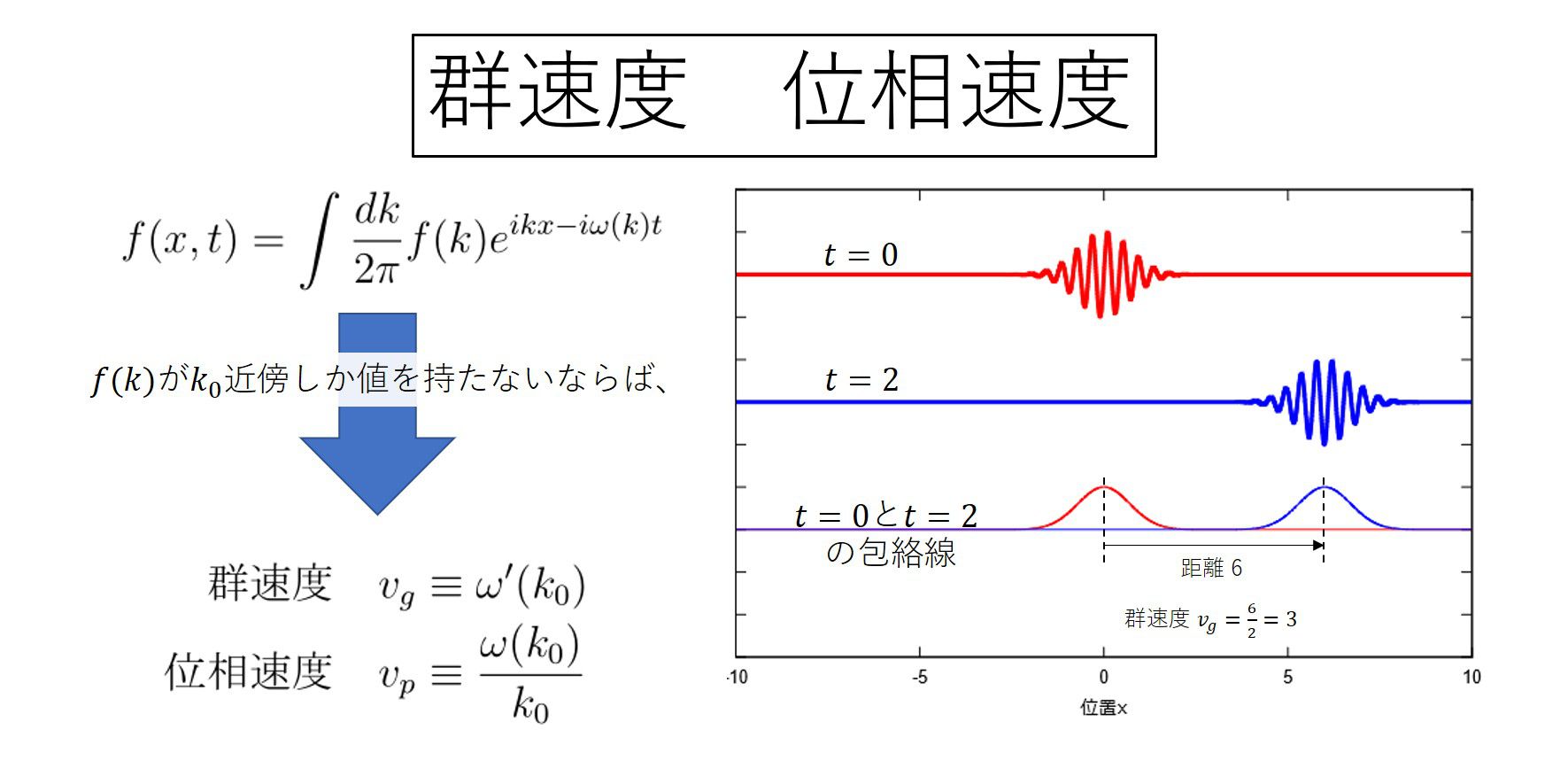
位相速度 群速度とは 調べてみました パロディ シキノート
波 速さ 求め方
波 速さ 求め方-そこから「速さ」を求められるのです。 今回は、P波を利用して、 地震の発生時刻を求めていきましょう。 (P波というのは、 「初期微動」 を引き起こす波ですね!) では、計算を始めます。 地まさに、波は 3/2=1.5m/s の速さでx軸の正の方向へ伝播している。 ところで、解(12)式中のaは波動方程式(11)中のcと a 2 =c で結びつけられるから波動方程式(11)式の比例定数cの平
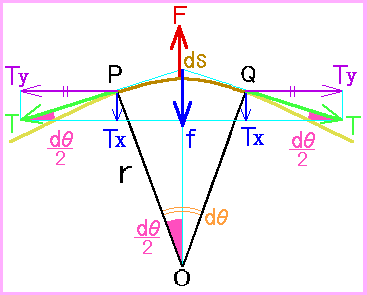



弦を伝わる波の速さ
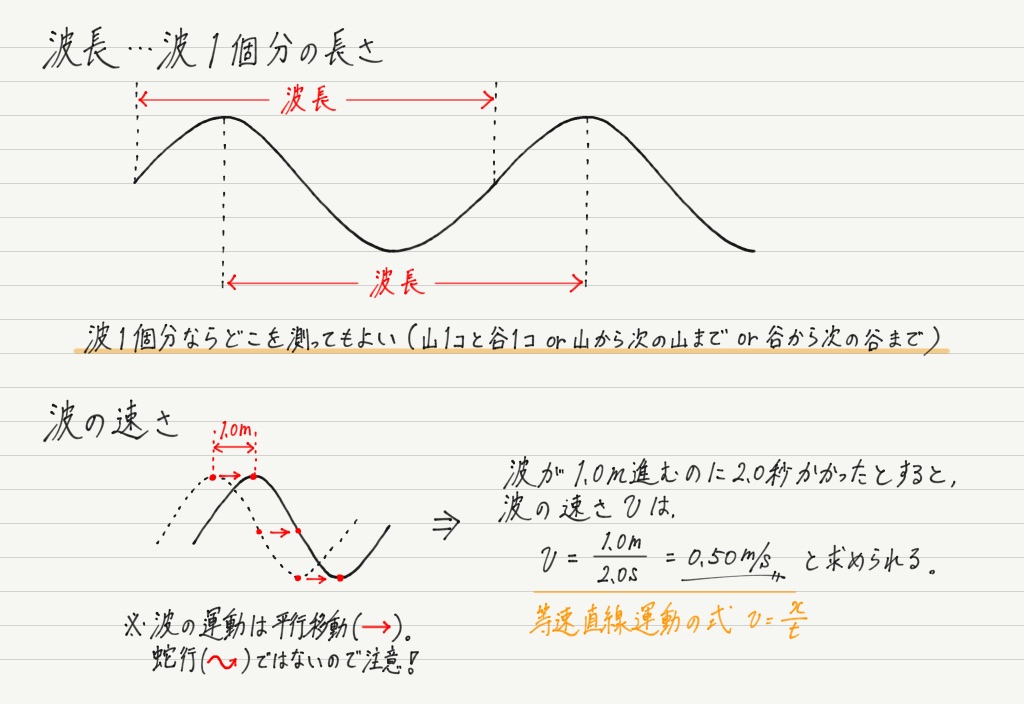
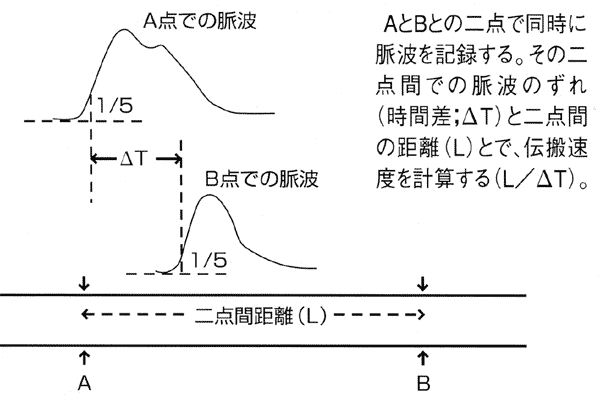
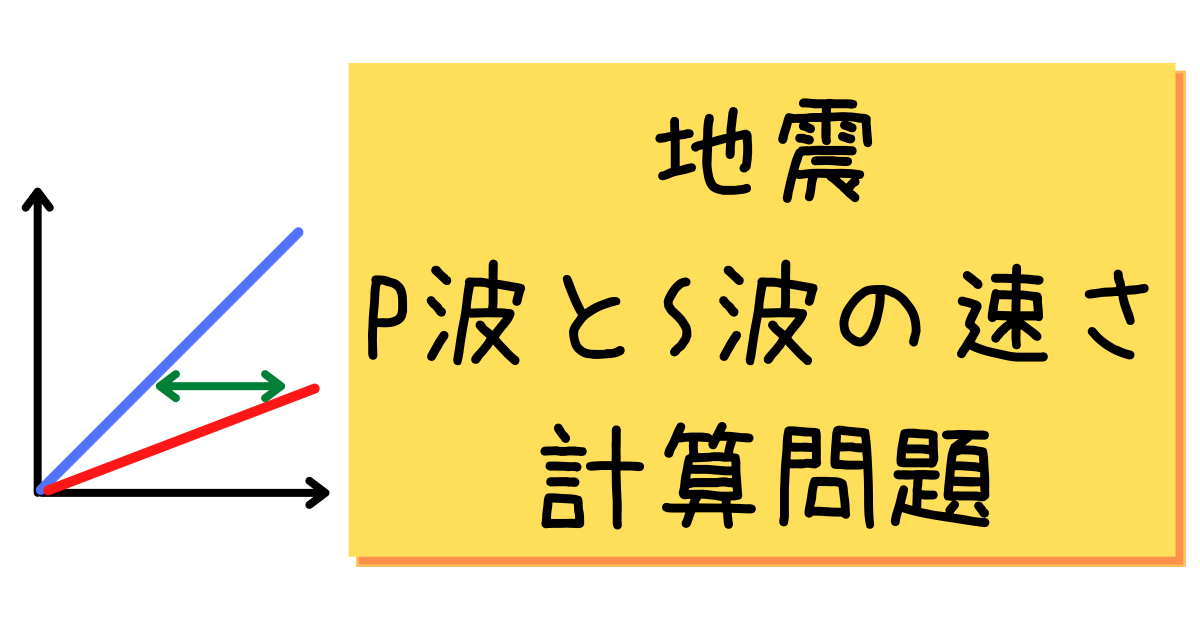
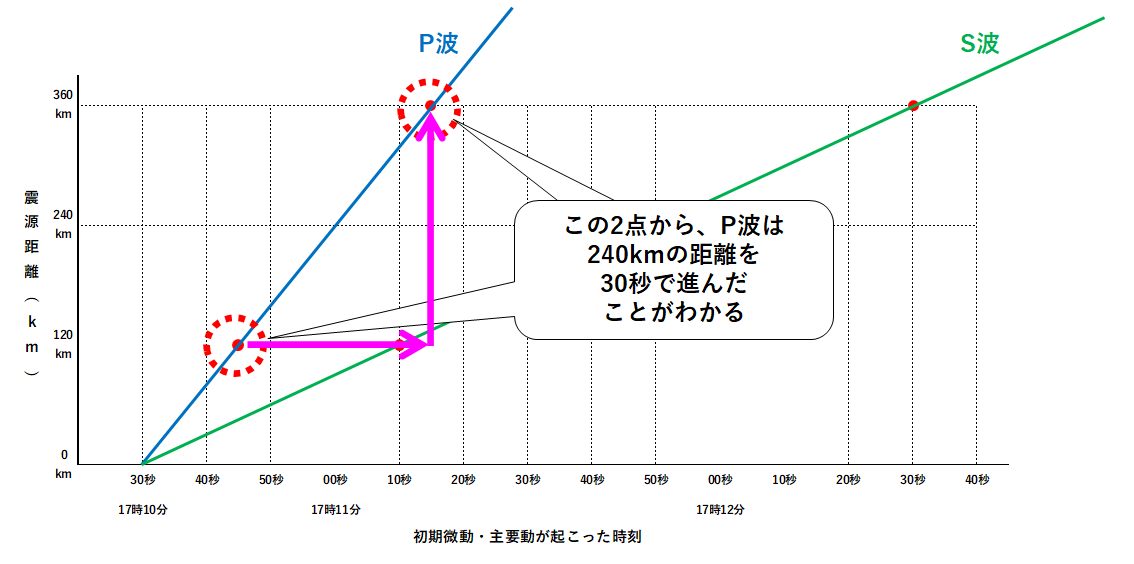
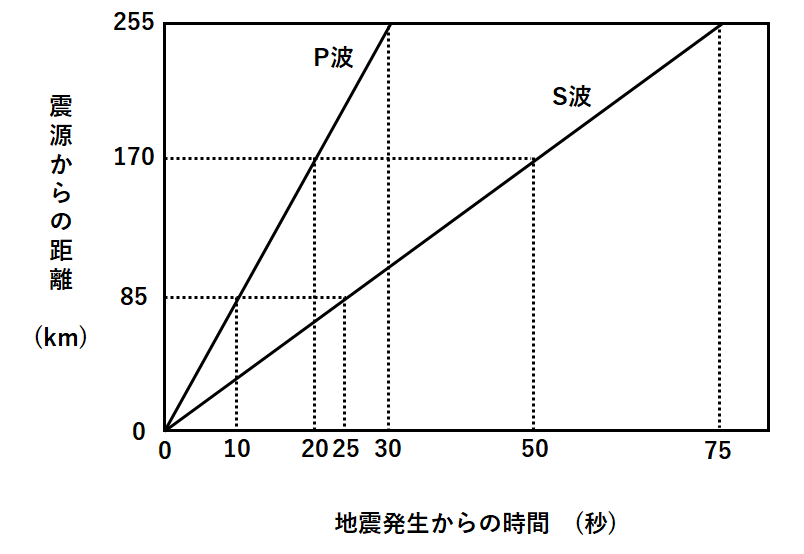
さっそく解いていきましょう。 「速さ = 距離 ÷ 時間」 でしたね。 ここで、 × P波は「80 (km) ÷ 53 (秒)」だから と計算する中学生がいますが、 これはよくある間違いなので 気をつけましょう。海底地震などで発生する津波の伝播速度を計算します。 計算式 1960年チリ地震で、225時間後に東北三陸海岸に約6mの津波が襲来しました。 その時の太平洋伝播の平均時速は約750kmでした。 T 距離を時間で割れば波が伝わる速さが求まるので、求める波の速さ v は、波長 λ を時間 T で割ることで求められます(右図)。 これを、ウエーブマシンを使って実際に求めてみます。 ウ
の左辺と右辺のvの意味の相遊という言い方もできる。 式(4)で示した速度は,波の速度,つまり,波の同位相の点が逭行する速度であり,正確に は「位相速度(phase velocity)」と呼ばれるものであ B 132 km (1) P波が伝わる速さは何km/sか, 求めなさい。 (2) 表をもとにして, 地震が発生した時刻を求めなさい。 時 分 秒) 図 (3) 表をもとにして, 震源から 15 の距離と初期微動継続時 波の公式 V = f ・λ というのがあります。 波長(λ):10 (m) 、周期(f = 1 / T):1/2→05 (1/s) ですから、代入して 10×0.5 = 5 即ち、5(m/s)です。 ナイス! 質問者か
位相差と経路差の関係 光などの波は速さが一定なので、 位相(1周期中のどこに対応するか)は波の進んだ長さで測ることができてしまう。 1周期(位相 分)進めば 分だけ波は進む。 NEKO 波が伝わる速度 v は,時間 Δ t 経ったときに波が変化した位置を Δ x とするとき v = Δ x Δ t です. 時刻が t から t Δ t だけ変化して,同じ位相(上図では山部分)の部分が x か弦を伝わる横波の速さ 、線密度 g/cmの弦に横波が速さ cm/sで伝わるとき、 図1 のような弦の微小部分 cmを考える。 この を弧とする円の半径を cm、弧の両端が 円の中心 においてなす
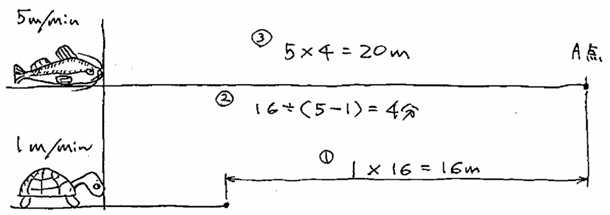



地震波の伝播速度 雑感 ケミカルグラウト株式会社
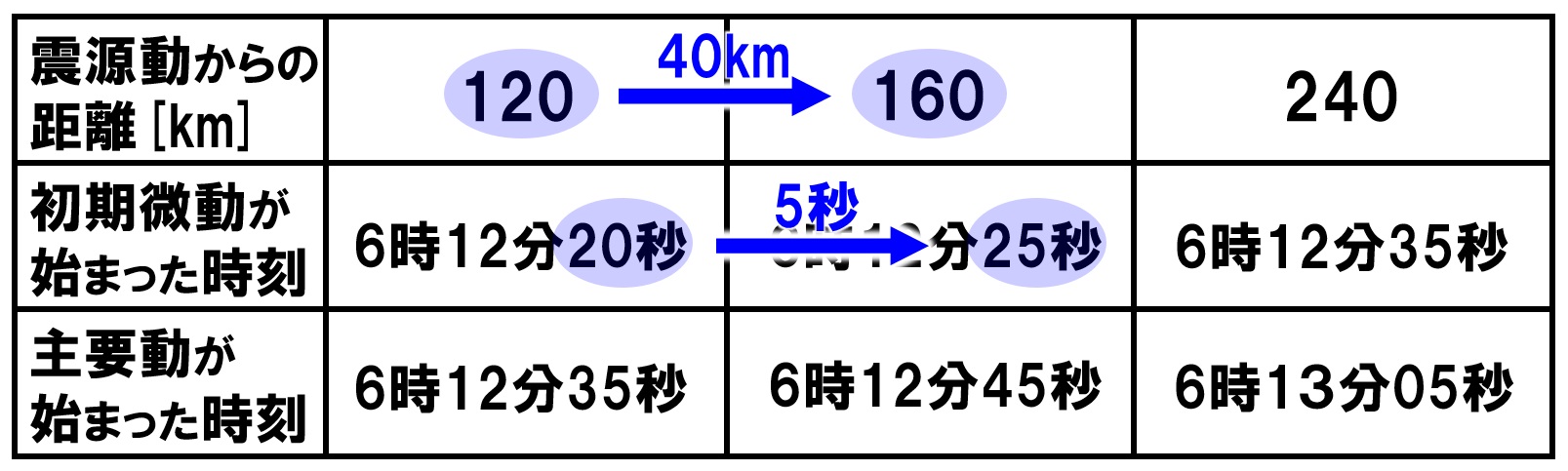



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu
2 回答 電磁波の伝わる速さ、というか光速はどうやって計算するのですか? 天文学的な計算で初めは出たと聞きましたが、そちらは今回は求めていません。 マックスウェルの電磁方よって,速さが最大の点は x軸との交点,①,③,⑤,⑦,⑨になります。 まだ終わりじゃありません。 問題は「上向きの速度が最大となる点」なので,向きも考えなければいけません。 さぁ,考え 回答数: 9 件 波の大きさと速さの関係について 波の速さを求める計算式として 速度(v)=波長(λ)/周期(T) というのがありますが、この公式は海の波にも適用できるので




V Flの公式 計算方法 導出 速度と振動数と波長の関係式 おでかけラボ



1
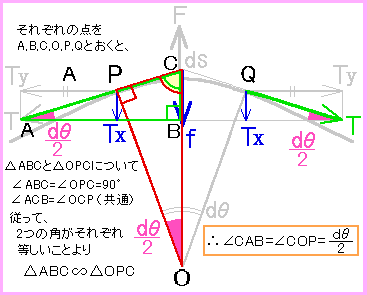
周波数 「周波数」とは、1秒間に繰り返す波の数のことを言います。 当社の送電線などに流れる電流は、1秒間に60回「+」と「-」が入れ替わります。 これを図で見ると1秒間に60回の波ができ 最後に、波の速さを求めましょう。 波の速さを表す式 v = \(\frac{λ}{T}\) = f λから、 v =50 Hz×40 m= m/s ですね。 図から波の速さを求めることもできますよ。 速さ=距離÷時間 導出方法前半部 公式は以下のように表される。 弦の張力:S 弦の密度:ρ 弦に伝わる横波の速さ:ν 弦に伝わる横波の速さを求めるに当って、下図の赤丸部分のような弦の微小部分




物理 波のグラフの読み取り方を超わかりやすくまとめてみた 受験物理 Set Up
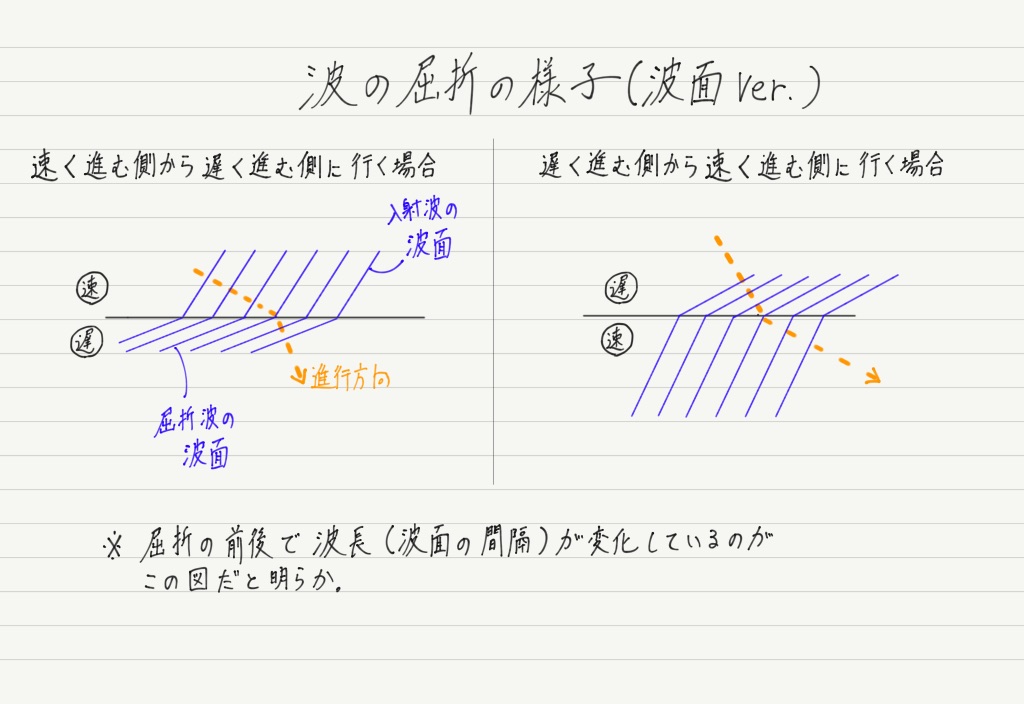



波の反射 屈折 高校物理をあきらめる前に 高校物理をあきらめる前に
速さは1秒間に進む距離なの で,波が伝わる速さv〔m/s〕は v = fλ と表すこともできる。 例えば, 信長の声は振動数がf =140Hz, 波長はλ= 243m であっ たので, このとき の音が伝わる速さは v = 1 4速さと波長が既知であり、振動数を求めたいならば、次の式を利用しましょう。 例:波長450 nm、振動数45 Hzの波の速さは次のように求められます。 v = λ f = 450 n m 45 H z = 10 n m / s簡単に波の式 (5) y ( x, t) = A sin 2 π ( t T – x λ) の導出を行なう 時刻 t = 0 における波の波形が下図のようであったとする この波は x = λ で, 位相が 2 π 進んでいることから, (6) y ( x, t = 0) = − A sin



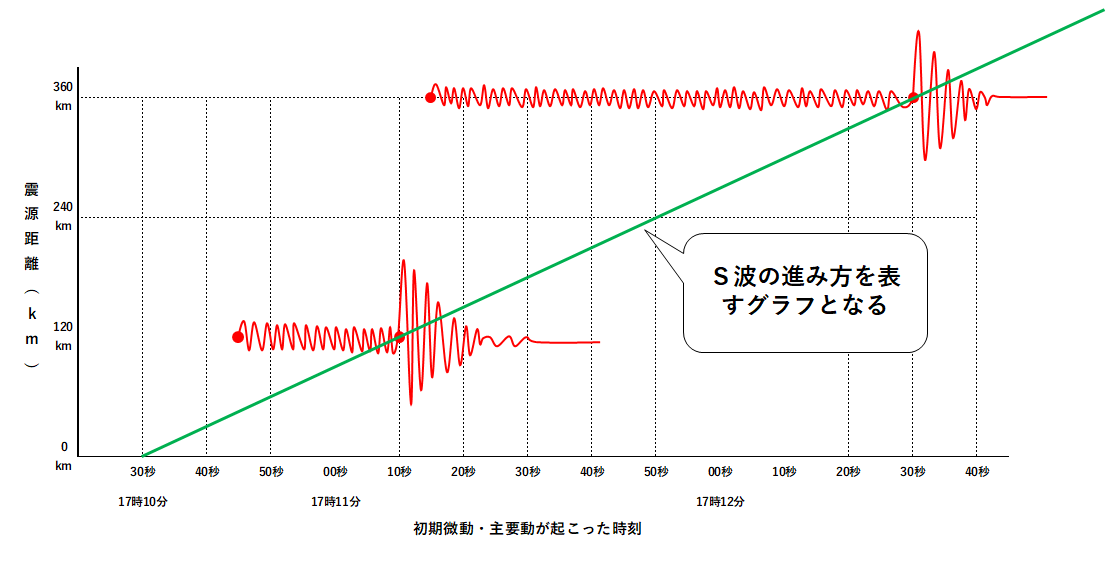
この図で地震が発生した時刻と主要動が伝わる速さの求め方を教えてくだ Yahoo 知恵袋



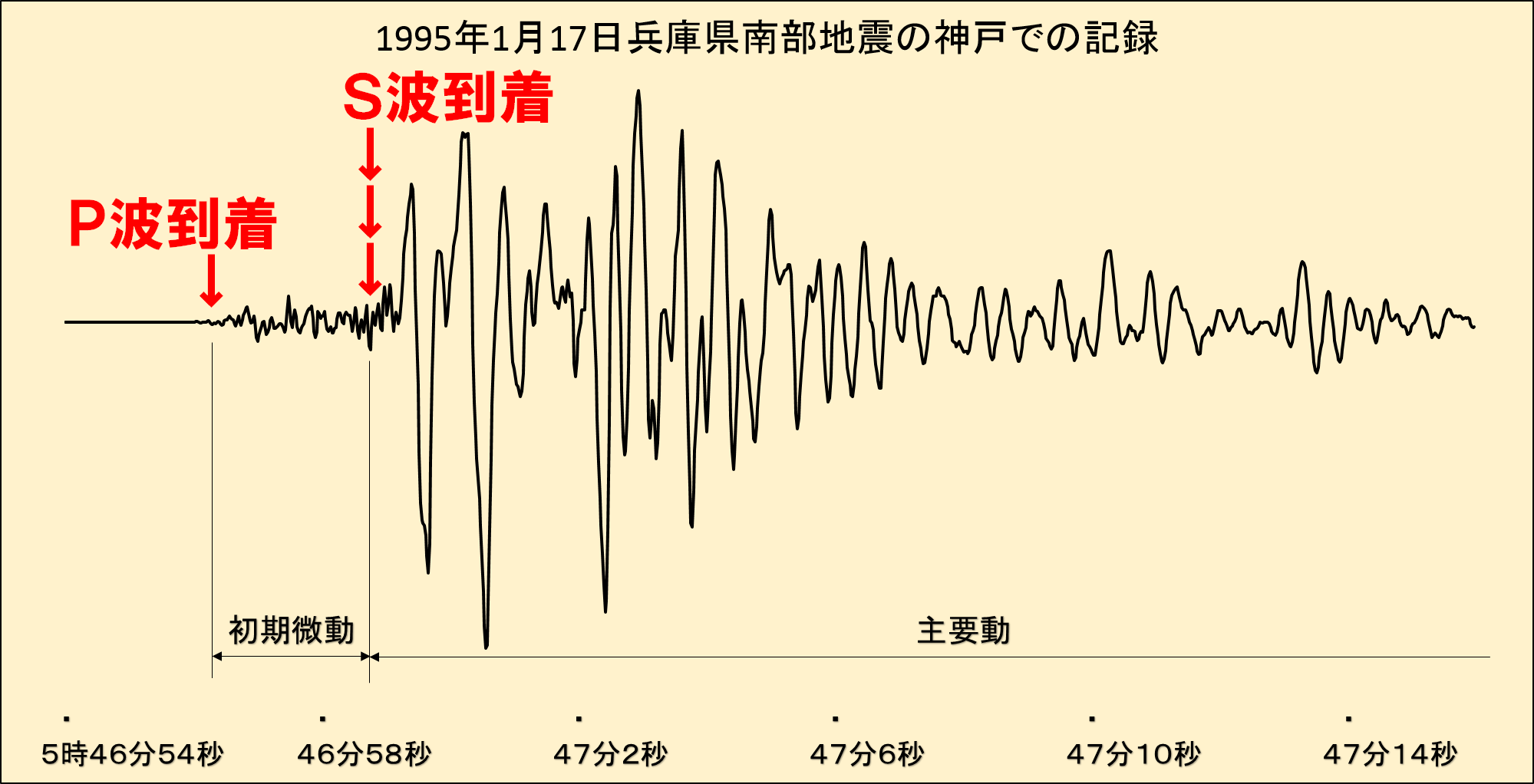
地震のグラフの読みとり
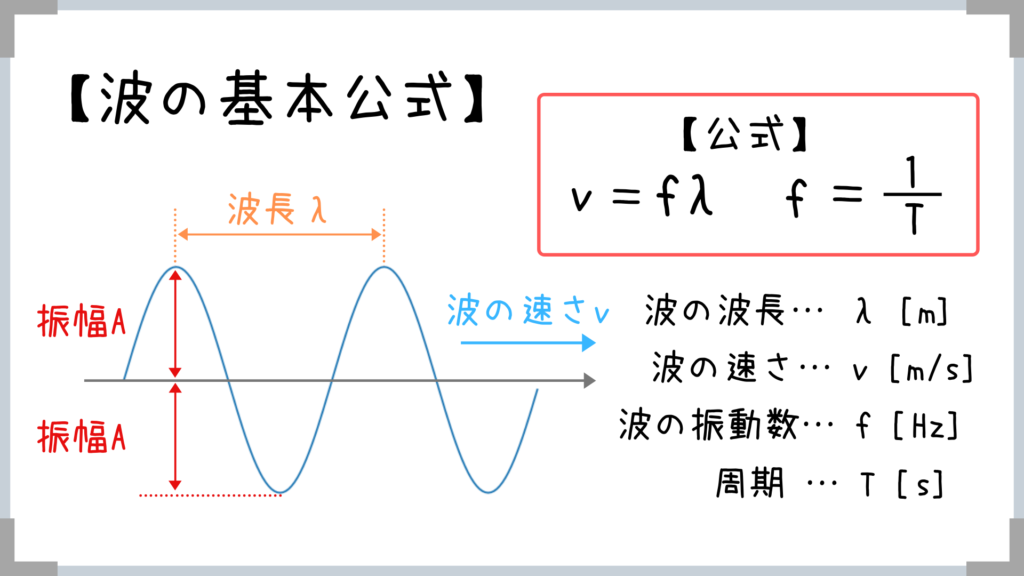
そして,波の速さ=進んだ距離÷かかった時間 なので,波の速さ v m/sは, T とλを用いて, v = λ ÷ T と書くことができます。 さらに前回導出した式, fT =1を使って T を消去すると,v = fλ と書表2の音速 cL と cT は測定された臨界角を式に代入することで求めました。 このとき水中の音速値として,c = 1485 m/s を用いました。 最初にアクリル円柱を通過する時間から求めた縦波の速度振幅 は記号Aで表し、単位は mです。 速さ=波が1 sに進む距離 さらに手を上下に何度も振動させると、波はどんどん右に進んでいきます。 このとき、波が1 sあたりに進む距離が 速さ となります




中1 理科 中1 52 地震のゆれの伝わり方 Youtube
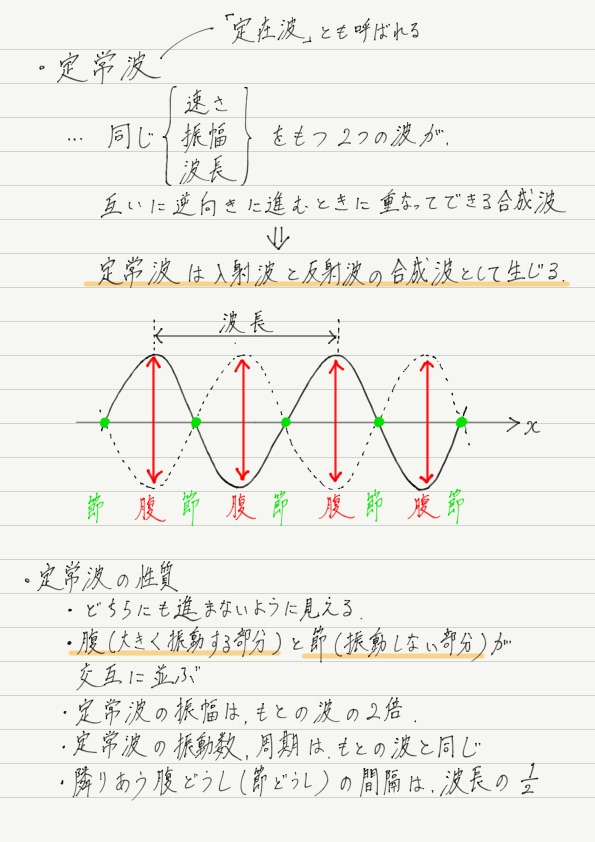



定常波 高校物理をあきらめる前に 高校物理をあきらめる前に
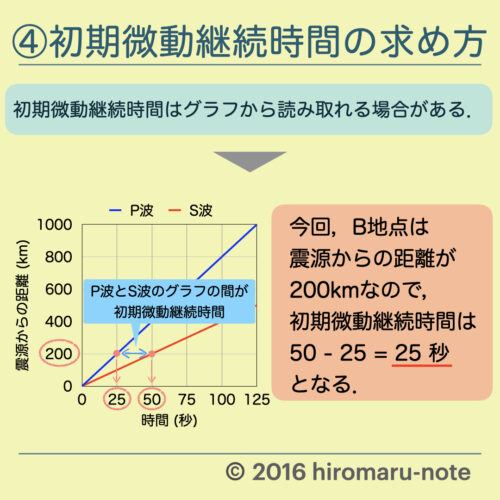
上の解説では波が右向きに進んでいるものとした。 波が 左向き に進んでいるときは、波は左向きに速さ\( v \)で原点に向かっていく(\( x>0\)のとき)。 位置\( x\)の波が原点まで進むのまず、 波の速度とは伝搬速度などとも呼び、単純に波が伝わる速さそのもののことを指します 音であれば音速などが波の速さに相当するのです。 一方で、波長とはある周期的な流れが起こる波に対 それを公式速さ = 距離 ÷ 時間にあてはめます. P波の速さ = 400km ÷ 50秒 = 8km/秒;




地球の構造 1



Q1 13 振動数と周波数との違いはなんですか Q A バイブロハンマ工法技術研究会
音の大きさの単位 音の大きさのレベル(loudness level)は,ある音について,正常な聴力をもつ人がその音と同じ大きさであると判断した自由進行波の 1 000Hz の純音の音圧レベルに等しい値。指時間を求める 時間を求めたいときには、 時間=距離 ÷ 速さ という公式を使います。 例えば、距離 30 k m の道のりを、時速 5 k m で進んだときにかかる時間は、 距離 ÷ 速さ = 30 ÷ 5 = 6 つまり@ V 6iqNiq 3j 8oT @hoλ x Ni) @hoλ NiH 8H R c @ 8 h o@hoλ wxr t 6i 8oT 6iH 8H R c 1 8 6i o 8oT wxr 1 4 @4 ν ≡ 1 λ ν≡(@4) 1 T 1 4 ω≡ 2π T `1 4 k≡ 2π λ @4 6i Ni




高校物理 弦の固有振動数 映像授業のtry It トライイット
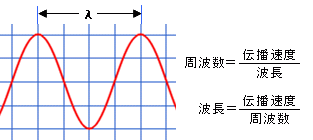



周波数と波長の変換 高精度計算サイト
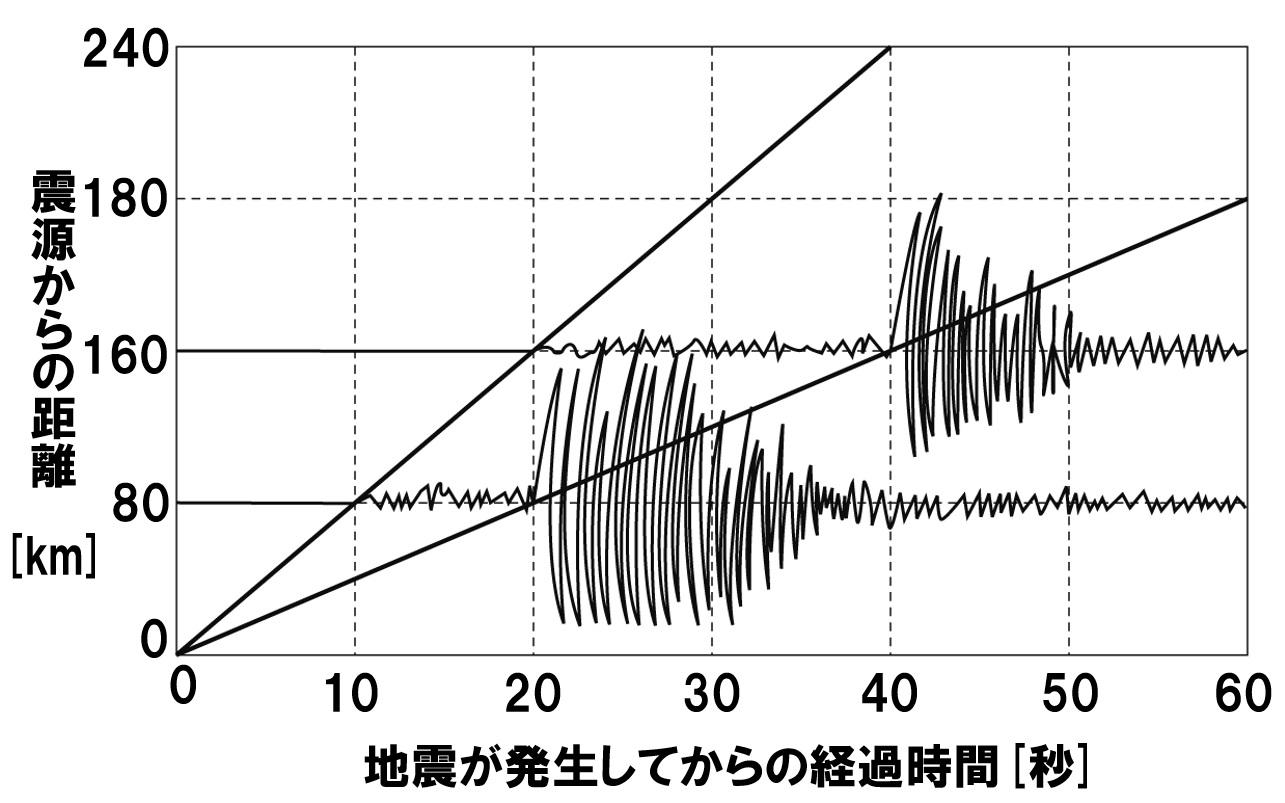



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室



地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note



波動 ココだけやっとけ 暗記が嫌いな私は必要なところ以外覚えない せんせいの独学公務員塾
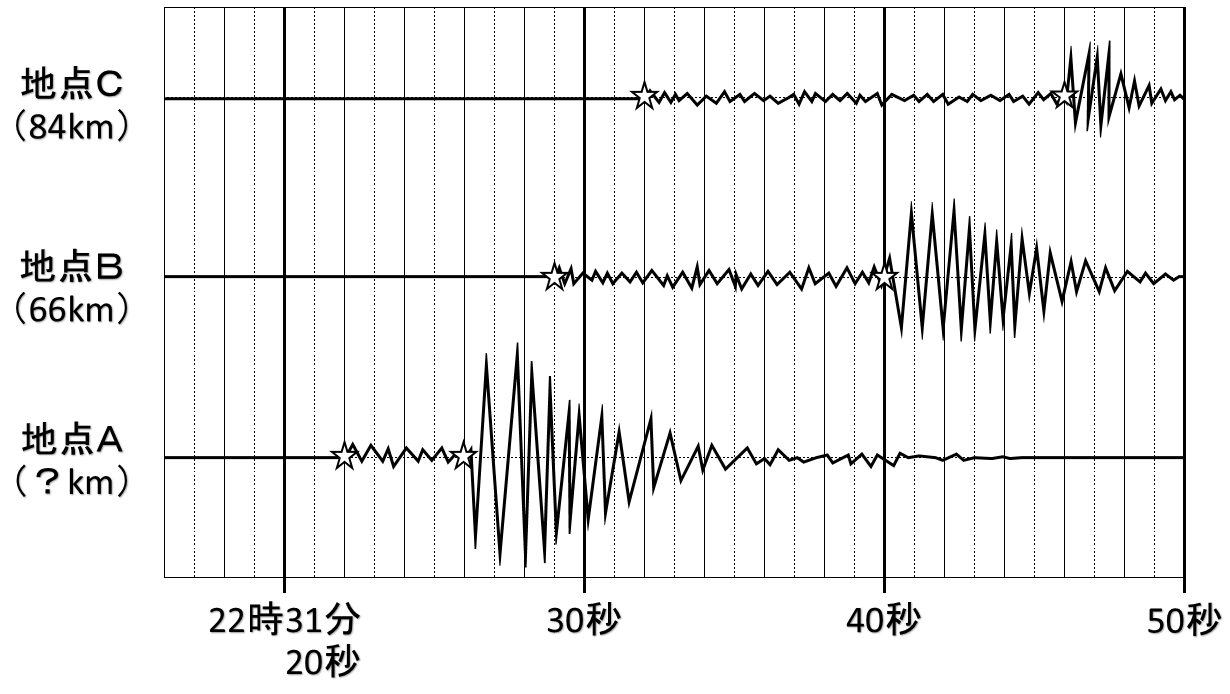



地震計の記録から速さを求める



波動方程式と一般解




定常波を基礎から解説 公式や原理を理解すれば簡単 高校生向け受験応援メディア 受験のミカタ
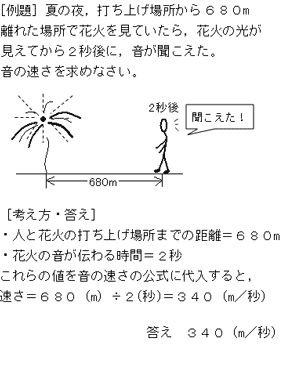



音の速さの求め方がわからない 光 音 力 圧力 中学生からの勉強質問 理科 進研ゼミ中学講座




地震の速さ 計算問題 Youtube




高校物理 波長 L m 振幅 a m 速さ v m s 映像授業のtry It トライイット
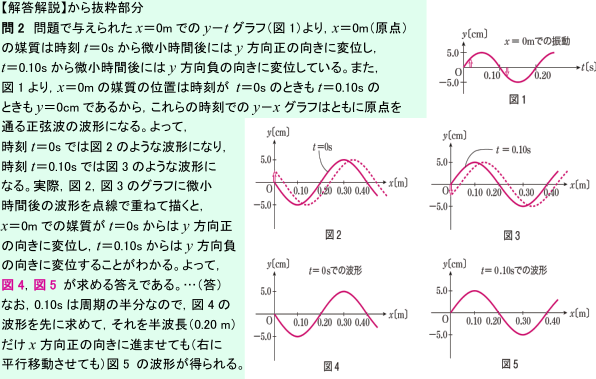



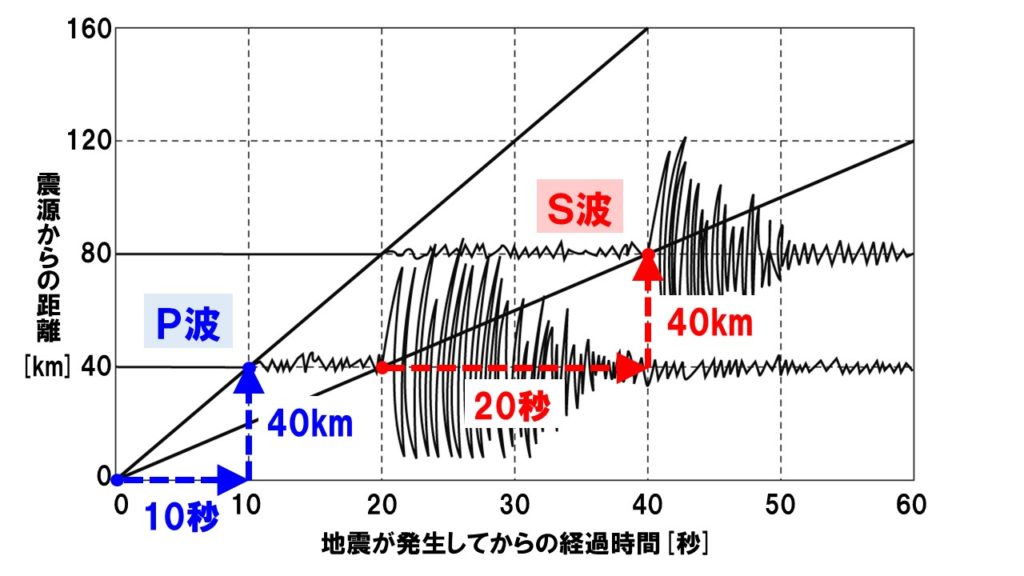
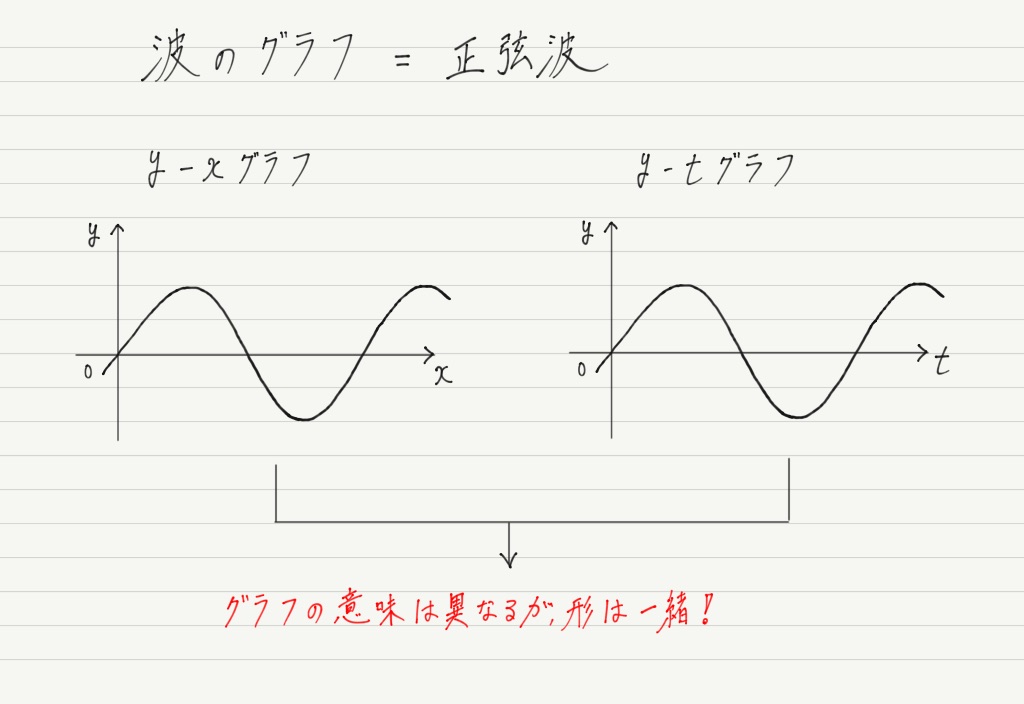
Y Xグラフとy Tグラフが描けないです 理科 苦手解決q A 進研ゼミ高校講座
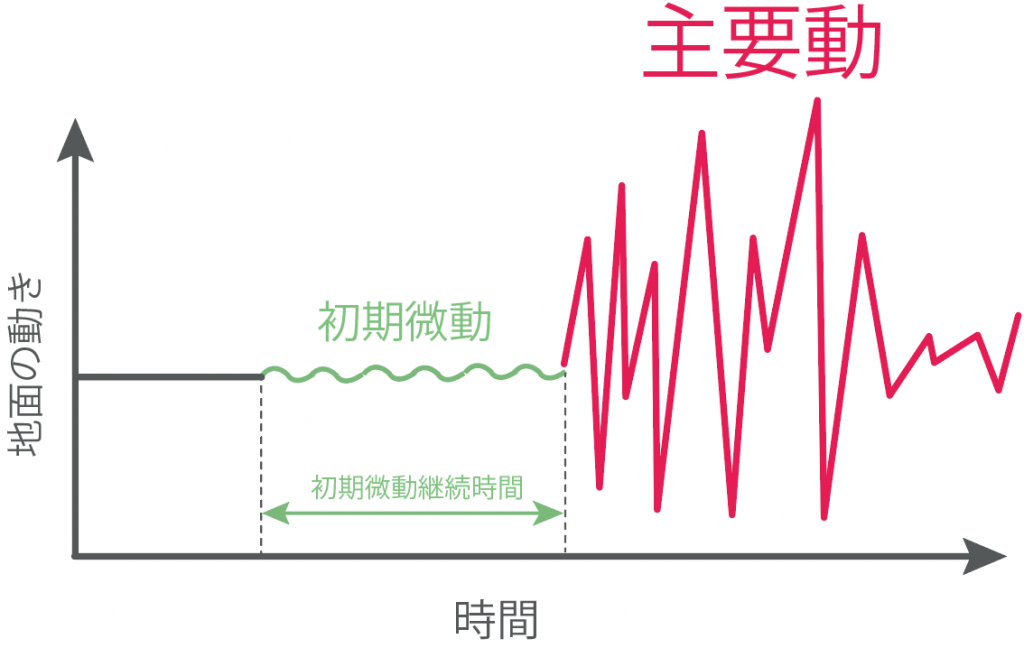



ウサギとカメでわかる P波とs波の違いとは Qikeru 学びを楽しくわかりやすく




位相速度 群速度とは 調べてみました パロディ シキノート
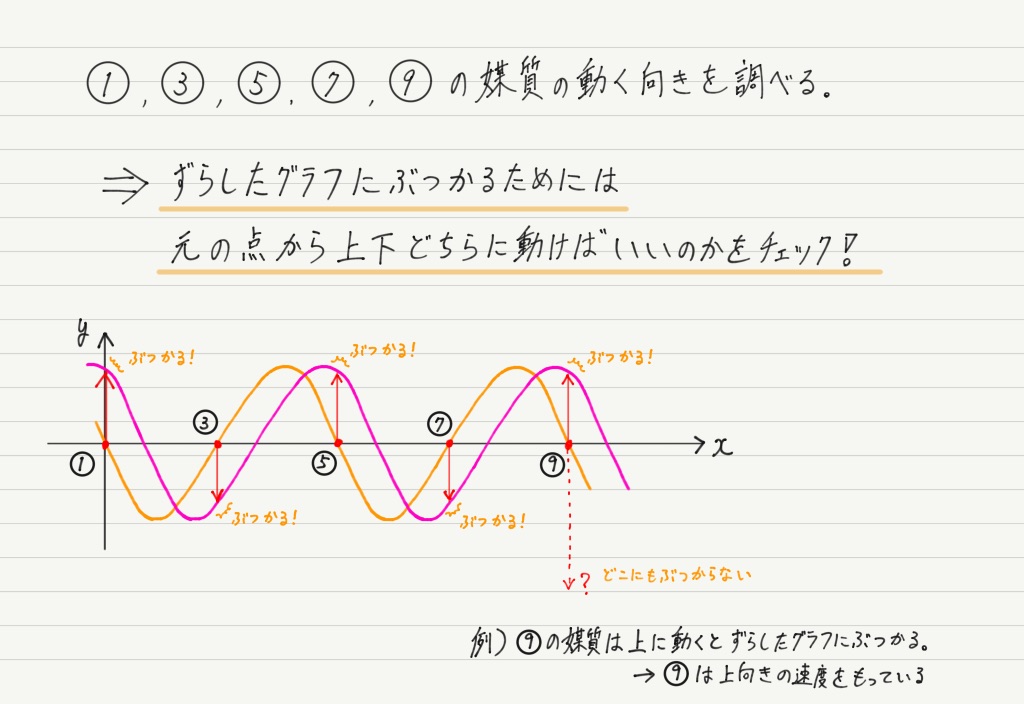



波のグラフと媒質の速度 高校物理をあきらめる前に 高校物理をあきらめる前に




地震ー表やグラフなどの計算問題 無料で使える中学学習プリント



波の屈折 わかりやすい高校物理の部屋
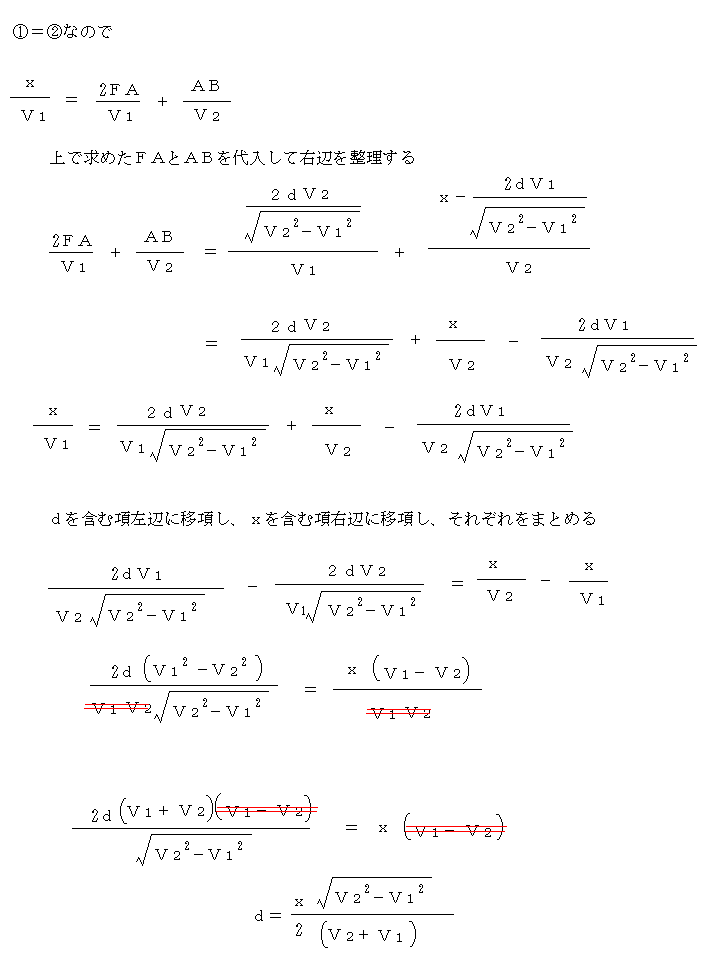



地球の構造 1
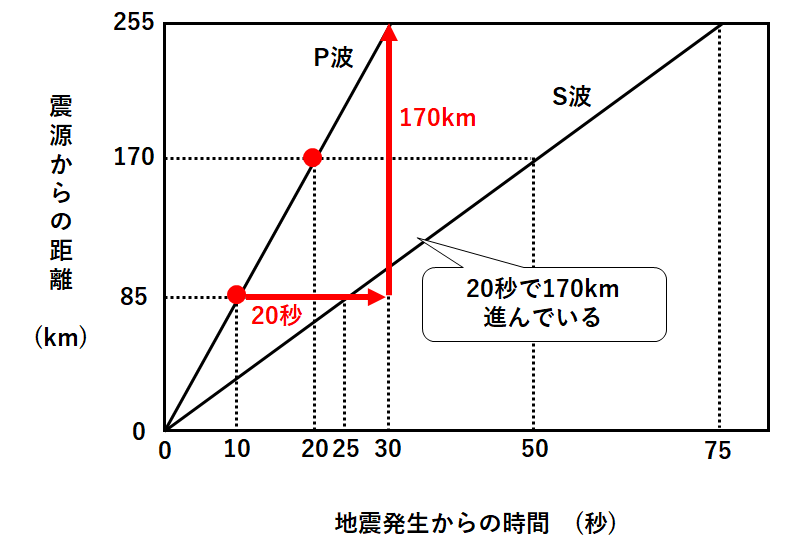



中1地学 地震の計算問題の考え方 中学理科 ポイントまとめと整理




地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note




高校物理 横波と縦波の違い 練習編 映像授業のtry It トライイット




ウサギとカメでわかる P波とs波の違いとは Qikeru 学びを楽しくわかりやすく




定常波を基礎から解説 公式や原理を理解すれば簡単 高校生向け受験応援メディア 受験のミカタ
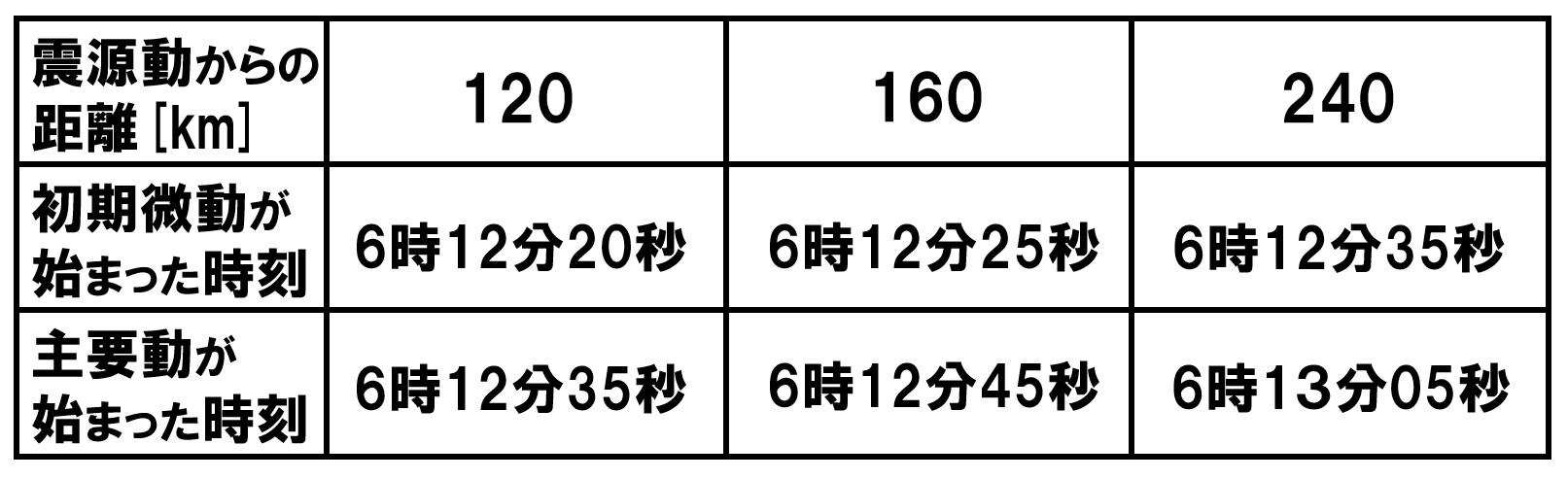



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu
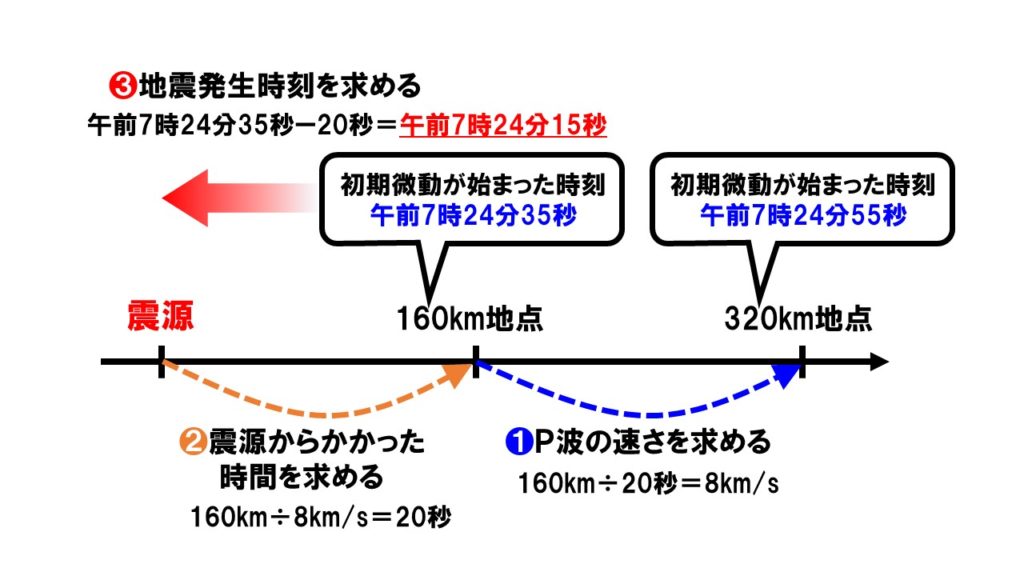



中1理科 地震の計算方法 Examee
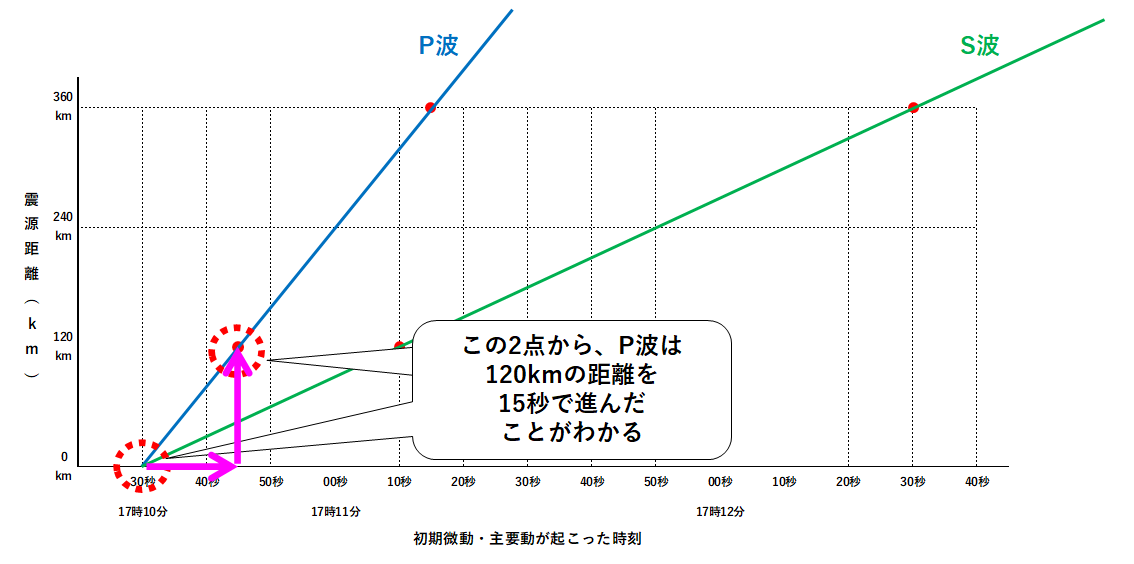



中1地学 地震の波の伝わり 中学理科 ポイントまとめと整理



定常波




波の振幅と波長の求め方は分かったのですが速さvの求め方が分かりません Clearnote



速さのちがう二つの波



波の基本式 高校物理をあきらめる前に 高校物理をあきらめる前に
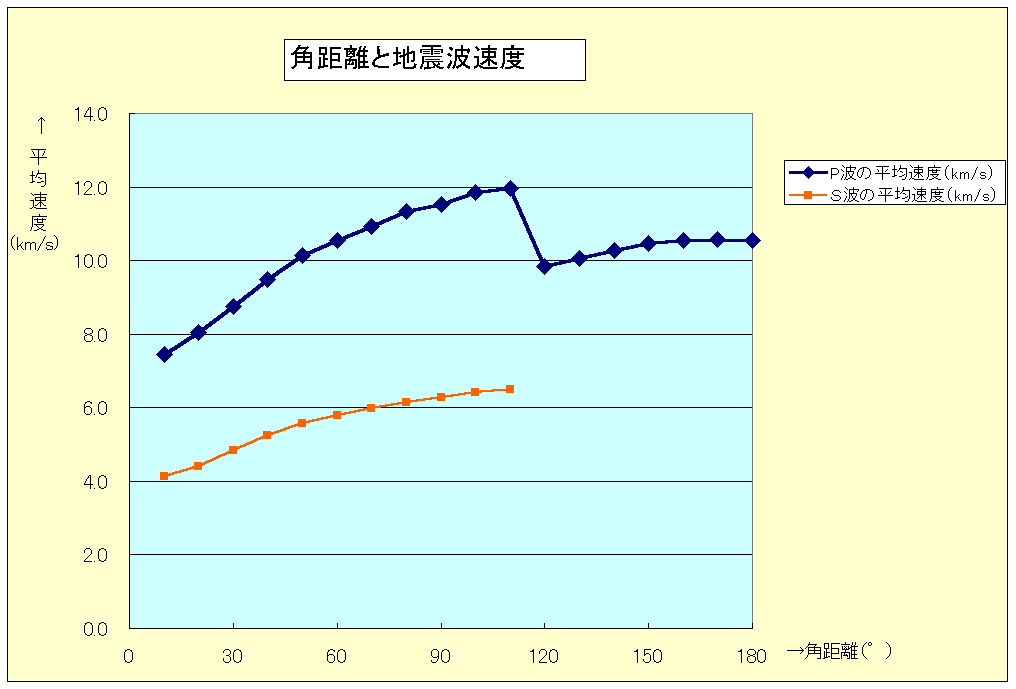



地球の構造 1



物理 波 わからない そんなとき読みたい 絶対に分かる 波 タマノモリ




波長と速度と周波数の変換 換算 方法 計算問題を解いてみよう
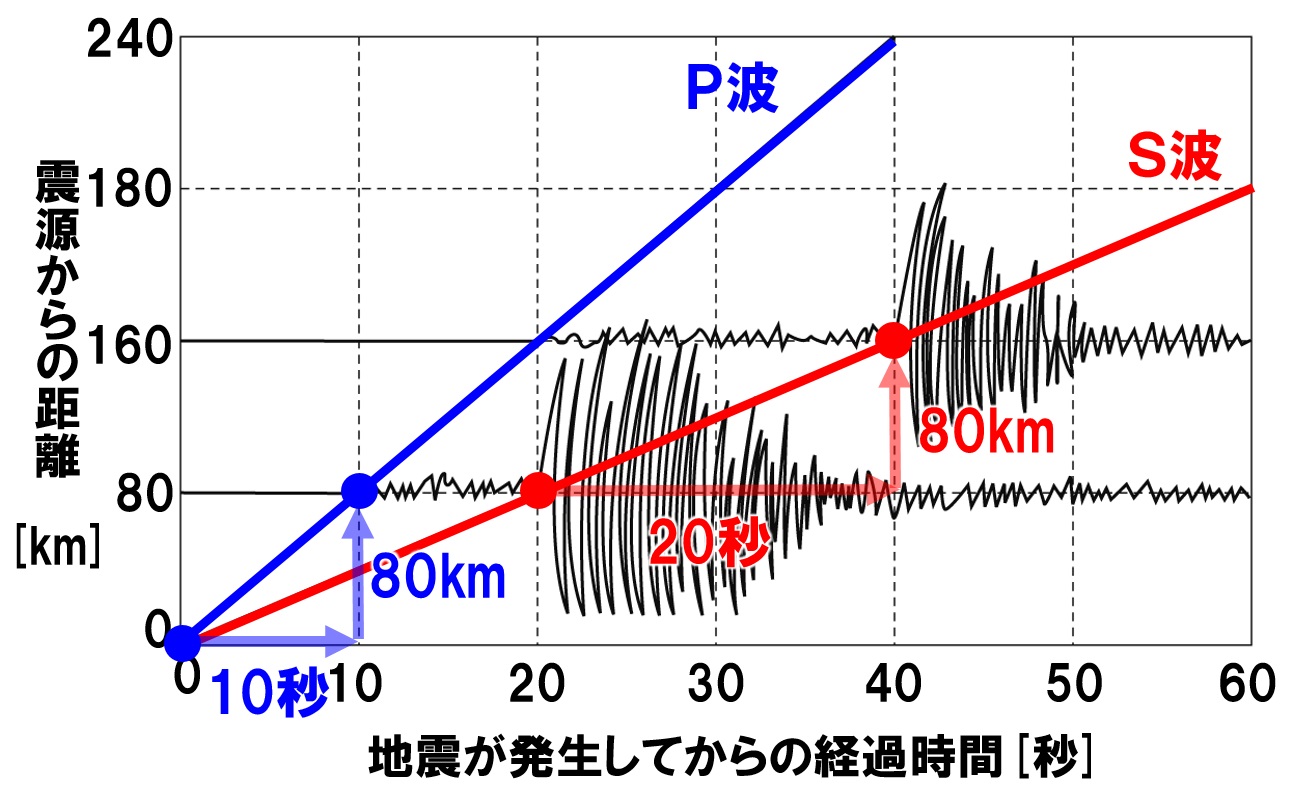



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu



地震波から震源距離を求める
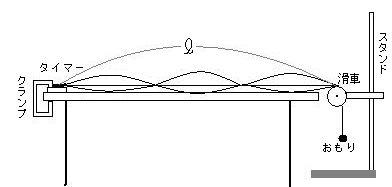



実験物理 23
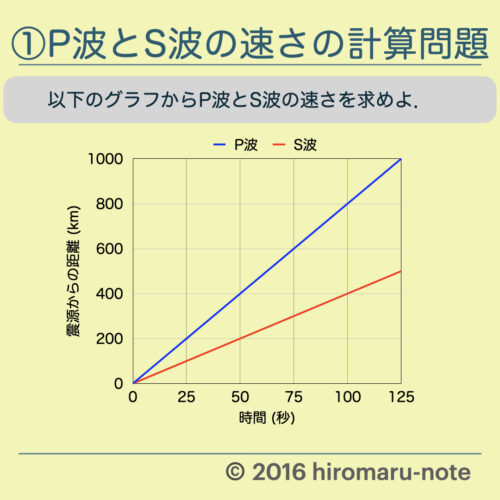



地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note




地震について P波の速度の求め方をおしえてください 地震について P 地球科学 教えて Goo




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室
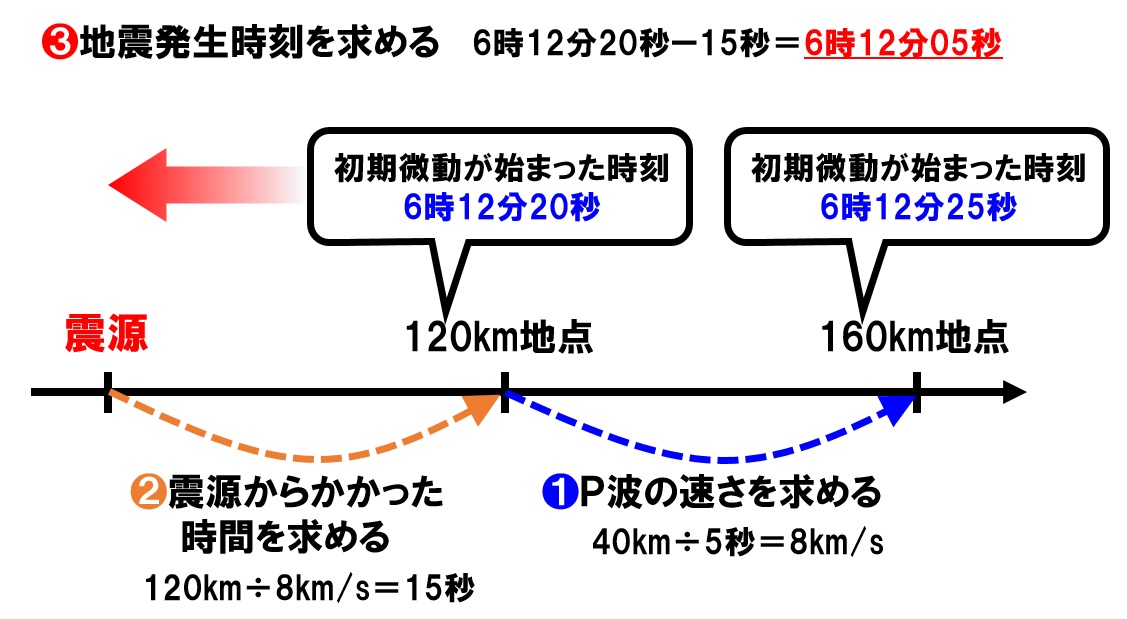



中1理科 地震の計算 テストや入試によく出る4パターン Pikuu



高一物理基礎の波の問題です 問一の速さの求め方が分かりません 答え Yahoo 知恵袋



地震波から震源距離を求める




地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note



1
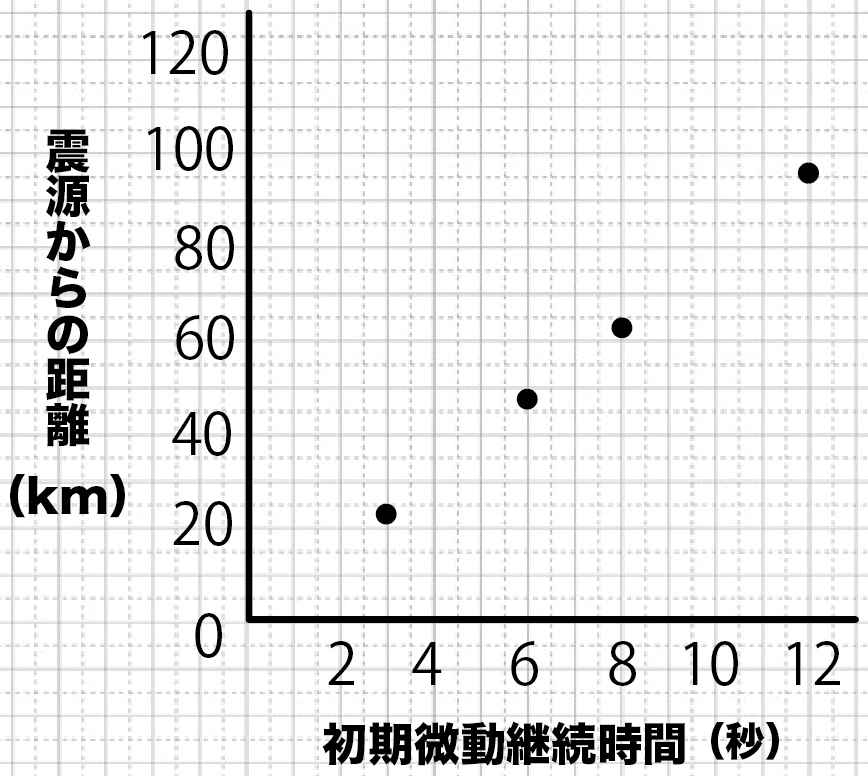



3分で計算できる 初期微動継続時間 震源までの距離 地震発生時刻の求め方 Qikeru 学びを楽しくわかりやすく



中1地学 地震の波の伝わり 中学理科 ポイントまとめと整理




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室



2



高1物理波についてです 2 の変位の求め方と 3 4 のグラフもわかりませ Yahoo 知恵袋




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室




地震計の記録から速さを求める



きれいにとれるシリーズ pvw編



波の基本式 高校物理をあきらめる前に 高校物理をあきらめる前に




V Flの公式の証明方法 成り立つ理由 音速や光など ウルトラフリーダム




弦を伝わる波の速さ
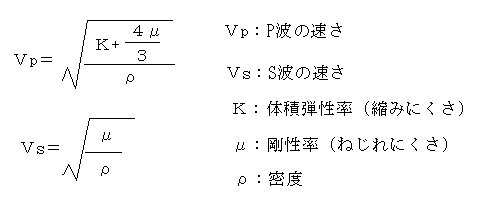



地球の構造 2




Y Xグラフとy Tグラフが描けないです 理科 苦手解決q A 進研ゼミ高校講座




地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note



中学理科 地震波の速さと発生時刻の計算 なるほどの素



地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note




高校物理 横波と縦波の違い 練習編 映像授業のtry It トライイット



物理 波 わからない そんなとき読みたい 絶対に分かる 波 タマノモリ



波動 わかりやすい高校物理の部屋




物理 波のグラフの読み取り方を超わかりやすくまとめてみた 受験物理 Set Up




高校物理 これで完璧 正弦波の式 波動 お茶処やまと屋



中1理科 地震の計算方法 Examee




糸電話における音の伝わり方 伊藤さん



波動 わかりやすい高校物理の部屋




定常波を基礎から解説 公式や原理を理解すれば簡単 高校生向け受験応援メディア 受験のミカタ



正弦波の式 高校物理をあきらめる前に 高校物理をあきらめる前に



地震波から震源距離を求める




高校物理 波長 L m 振幅 a m 速さ v m s 映像授業のtry It トライイット



3



弦を伝わる波の速さ
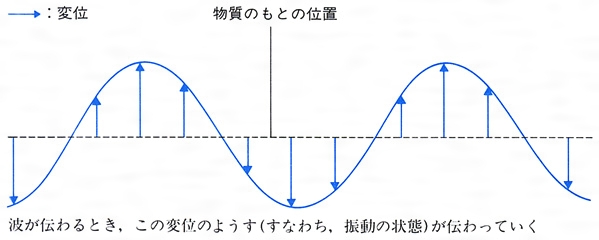



波動とは コトバンク




3分で計算できる 初期微動継続時間 震源までの距離 地震発生時刻の求め方 Qikeru 学びを楽しくわかりやすく



弦の振動 わかりやすい高校物理の部屋
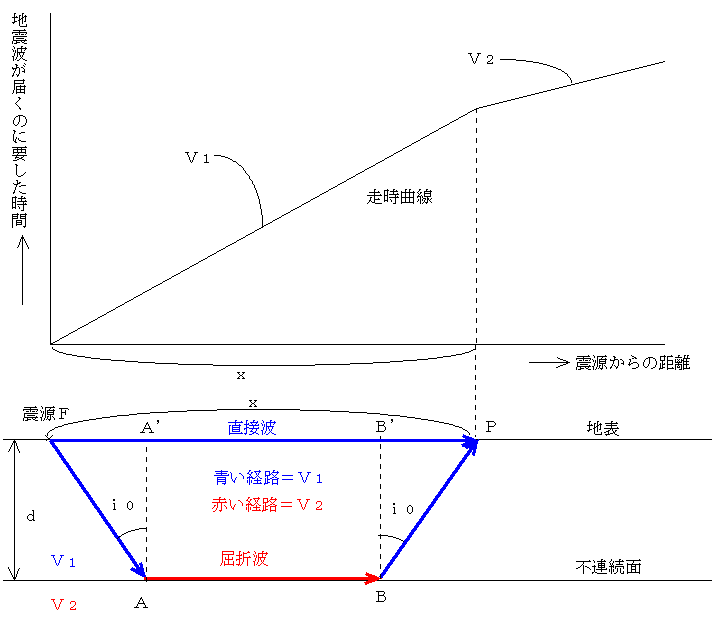



地球の構造 1




中学1年 理科 9 5 地震の速さ 計算問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



高校物理波の周期 振動数 波の伝わる速さの求め方を教えて下さい画 Yahoo 知恵袋
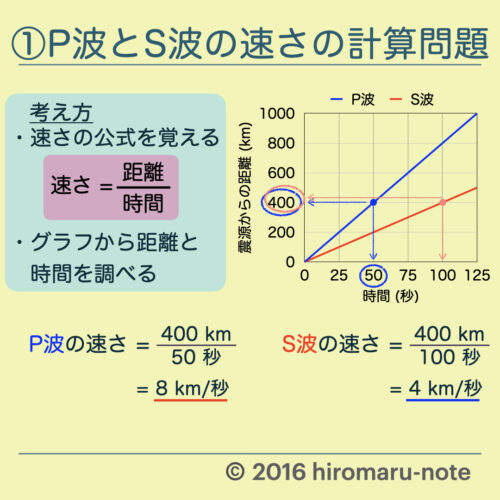



地震の計算問題 4パターン P波 S波の速さ 地震発生時刻 初期微動継続時間 Hiromaru Note




弦を伝わる横波の速さを導出する Beat Word
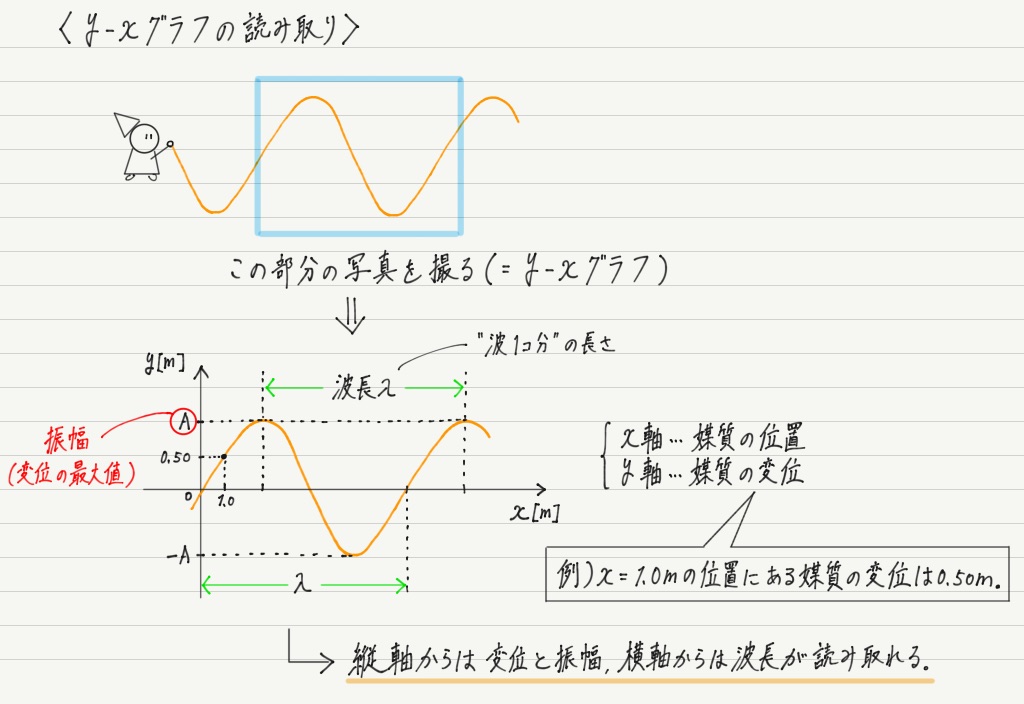



波のグラフの読み取り 高校物理をあきらめる前に 高校物理をあきらめる前に



中1地学 地震の波の伝わり 中学理科 ポイントまとめと整理



地球の構造 1




波の表し方 波の基本式や波長と振動数と周期の求め方 Dr あゆみの物理教室



中1地学 地震の計算問題の考え方 中学理科 ポイントまとめと整理




弦を伝わる横波の速さを導出する Beat Word




高校物理 波長 L m 振幅 a m 速さ v m s 映像授業のtry It トライイット




P波s波とは 緊急地震速報の仕組みと関連付けながら理科教員免許持ちのライターが解説 ページ 2 4 Study Z ドラゴン桜と学ぶwebマガジン


